PageRank

Introduction

PageRank is an algorithm that measures the importance of each node within the graph based on the number of incoming relationships and the importance of the corresponding source nodes. The algorithm was originally developed by Google’s founders Larry Page and Sergey Brin during their time at Stanford University.

Algorithm Overview

PageRank works by counting the number and quality of relationships to a node to determine a rough estimate of how important that node is. The underlying assumption is that more important nodes are likely to receive more connections from other nodes.

The algorithm assigns each node a score, where higher scores indicate greater importance. The score for a node is derived recursively from the scores of the nodes that link to it, with a damping factor typically applied to prevent rank sinks. For example, in a network of academic papers, a paper cited by many other highly cited papers will receive a high PageRank score, reflecting its influence in the field.

Syntax

The PageRank procedure has the following call signature:

CALL pagerank.stream(
    [label],
    [relationship]
)
YIELD node, score

Parameters

Name	Type	Default	Description
`label`	String	null	The label of nodes to run the algorithm on. If null, all nodes are used.
`relationship`	String	null	The relationship type to traverse. If null, all relationship types are used.

Yield

Name	Type	Description
`node`	Node	The node processed by the algorithm.
`score`	Float	The PageRank score for the node.

Examples

Unweighted PageRank

First, let’s create a sample graph representing a citation network between scientific papers:

CREATE 
  (paper1:Paper {title: 'Graph Algorithms in Database Systems'}),
  (paper2:Paper {title: 'PageRank Applications'}),
  (paper3:Paper {title: 'Data Mining Techniques'}),
  (paper4:Paper {title: 'Network Analysis Methods'}),
  (paper5:Paper {title: 'Social Network Graph Theory'}),
  
  (paper2)-[:CITES]->(paper1),
  (paper3)-[:CITES]->(paper1),
  (paper3)-[:CITES]->(paper2),
  (paper4)-[:CITES]->(paper1),
  (paper4)-[:CITES]->(paper3),
  (paper5)-[:CITES]->(paper2),
  (paper5)-[:CITES]->(paper4)

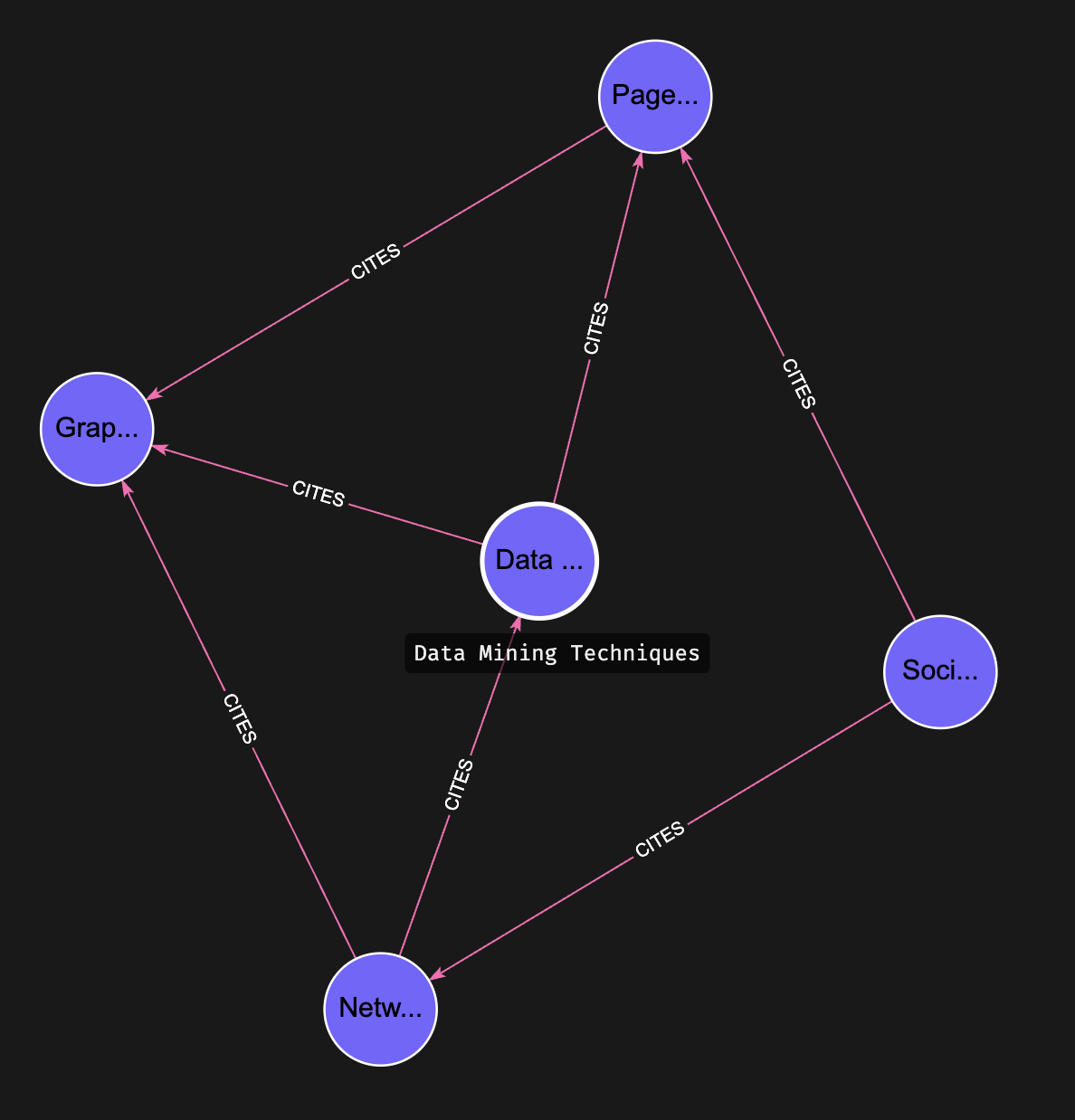
Graph PR

Now we can run the PageRank algorithm on this citation network:

CALL pagerank.stream('Paper', 'CITES')
YIELD node, score
RETURN node.title AS paper, score
ORDER BY score DESC

Expected results:

paper	score
Graph Algorithms in Database Systems	0.43
Data Mining Techniques	0.21
PageRank Applications	0.19
Network Analysis Methods	0.14
Social Network Graph Theory	0.03

Usage Notes

Interpreting scores:

PageRank scores are relative, not absolute measures
The sum of all scores in a graph equals 1.0
Scores typically follow a power-law distribution