Path algorithms
In v2.10 introduced two new path-finding algorithms, or more accurately, minimum-weight, optionally bounded-cost, and optionally bounded-length path-finding algorithms, algo.SPpaths and algo.SSpaths.
algo.SPpaths and algo.SSpaths can solve a wide range of real-world problems, where minimum-weight paths need to be found. algo.SPpaths finds paths between a given pair of nodes, while algo.SSpaths finds paths from a given source node. Weight can represent time, distance, price, or any other measurement. A bound can be set on another property (e.g., finding a minimum-time bounded-price way to reach from point A to point B). Both algorithms are performant and have low memory requirements.
For both algorithms, you can set:
-
A list of relationship types to traverse (
relTypes). -
The relationships’ property whose sum you want to minimize (
weight). -
A optional relationships’ property whose sum you want to bound (
cost) and the optional bound (maxCost). -
An optional bound on the path length - the number of relationships along the path (
maxLen). -
The number of paths you want to retrieve: either all minimal-weight paths (
pathCountis 0), a single minimal-weight path (pathCountis 1), or n minimal-weight paths with potentially different weights (pathCountis n).
This topic explains which problems you can solve using these algorithms and demonstrates how to use them.
Let’s start with the following graph.
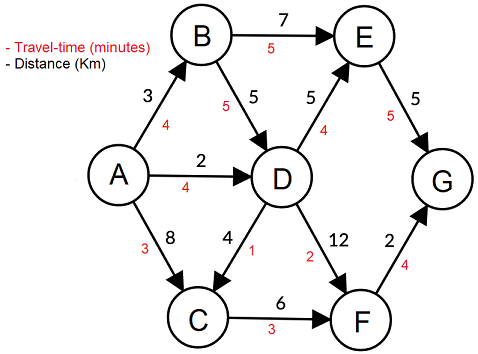
This graph represents a road network with 7 cities (A, B, C, and so on) and 11 one-way roads. Each road has a distance (say, in kilometers) and trip time (say, in minutes).
Let’s create the graph.
GRAPH.QUERY g "CREATE (a:City{name:'A'}), (b:City{name:'B'}), (c:City{name:'C'}), (d:City{name:'D'}), (e:City{name:'E'}), (f:City{name:'F'}), (g:City{name:'G'}), (a)-[:Road{time:4, dist:3}]->(b), (a)-[:Road{time:3, dist:8}]->(c), (a)-[:Road{time:4, dist:2}]->(d), (b)-[:Road{time:5, dist:7}]->(e), (b)-[:Road{time:5, dist:5}]->(d), (d)-[:Road{time:4, dist:5}]->(e), (c)-[:Road{time:3, dist:6}]->(f), (d)-[:Road{time:1, dist:4}]->(c), (d)-[:Road{time:2, dist:12}]->(f), (e)-[:Road{time:5, dist:5}]->(g), (f)-[:Road{time:4, dist:2}]->(g)"
If you’re using RedisInsight v2, you can create and visualize the graph by slightly modifying the above query: you’ll have to assign aliases to all nodes and relationships, and return them:
GRAPH.QUERY g "CREATE (a:City{name:'A'}), (b:City{name:'B'}), (c:City{name:'C'}), (d:City{name:'D'}), (e:City{name:'E'}), (f:City{name:'F'}), (g:City{name:'G'}), (a)-[r1:Road{time:4, dist:3}]->(b), (a)-[r2:Road{time:3, dist:8}]->(c), (a)-[r3:Road{time:4, dist:2}]->(d), (b)-[r4:Road{time:5, dist:7}]->(e), (b)-[r5:Road{time:5, dist:5}]->(d), (d)-[r6:Road{time:4, dist:5}]->(e), (c)-[r7:Road{time:3, dist:6}]->(f), (d)-[r8:Road{time:1, dist:4}]->(c), (d)-[r9:Road{time:2, dist:12}]->(f), (e)-[r10:Road{time:5, dist:5}]->(g), (f)-[r11:Road{time:4, dist:2}]->(g) RETURN a,b,c,d,e,f,g,r1,r2,r3,r4,r5,r6,r7,r8,r9,r10,r11"
Before v2.10
Before v2.10, you were able to solve these queries:
- Find the shortest path (by number of roads) from A to G
- Find all the shortest paths (by number of roads) from A to G
- Find 5 shortest paths (by number of roads) from A to G
- Find 5 shortest paths (in kilometers) from A to G
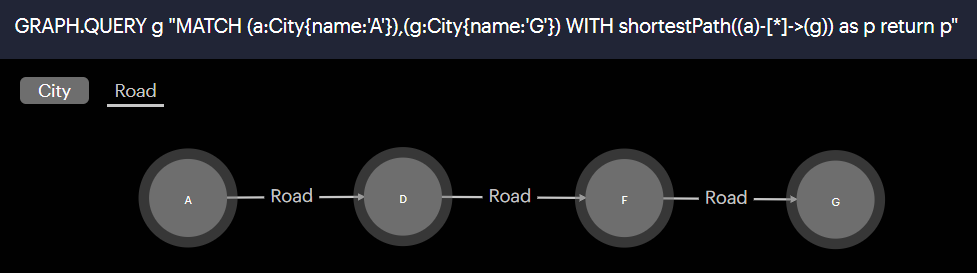
Find the shortest path (by number of roads) from A to G
GRAPH.QUERY g "MATCH (a:City{name:'A'}),(g:City{name:'G'}) WITH shortestPath((a)-[*]->(g)) as p RETURN length(p), [n in nodes(p) | n.name] as pathNodes"
1) 1) "length(p)"
2) "pathNodes"
2) 1) 1) (integer) 3
2) "[A, D, F, G]"
shortestPath returns one of the shortest paths. If there is more than one, only one is retrieved.
With RedisInsight v2, you can visualize a path simply by returning it.
Find all the shortest paths (by number of roads) from A to G
GRAPH.QUERY g "MATCH (a:City{name:'A'}),(g:City{name:'G'}) WITH a,g MATCH p=allShortestPaths((a)-[*]->(g)) RETURN length(p), [n in nodes(p) | n.name] as pathNodes"
1) 1) "length(p)"
2) "pathNodes"
2) 1) 1) (integer) 3
2) "[A, D, F, G]"
2) 1) (integer) 3
2) "[A, C, F, G]"
3) 1) (integer) 3
2) "[A, D, E, G]"
4) 1) (integer) 3
2) "[A, B, E, G]"
All allShortestPaths results have, by definition, the same length (number of roads).
Find 5 shortest paths (by number of roads) from A to G
GRAPH.QUERY g "MATCH p = (a:City{name:'A'})-[*]->(g:City{name:'G'}) RETURN length(p), [n in nodes(p) | n.name] as pathNodes ORDER BY length(p) LIMIT 5"
1) 1) "length(p)"
2) "pathNodes"
2) 1) 1) (integer) 3
2) "[A, B, E, G]"
2) 1) (integer) 3
2) "[A, D, E, G]"
3) 1) (integer) 3
2) "[A, D, F, G]"
4) 1) (integer) 3
2) "[A, C, F, G]"
5) 1) (integer) 4
2) "[A, D, C, F, G]"
Using the unbounded traversal pattern (a:City{name:'A'})-[*]->(g:City{name:'G'}), FalkorDB traverses all possible paths from A to G. ORDER BY length(p) LIMIT 5 ensures that you collect only [up to 5 shortest paths (minimal number of relationships). This approach is very inefficient because all possible paths would have to be traversed. Ideally, you would want to abort some traversals as soon as you are sure they would not result in the discovery of shorter paths.
Find 5 shortest paths (in kilometers) from A to G
In a similarly inefficient manner, you can traverse all possible paths and collect the 5 shortest paths (in kilometers).
GRAPH.QUERY g "MATCH p = (a:City{name:'A'})-[*]->(g:City{name:'G'}) WITH p,reduce(dist=0, n IN relationships(p) | dist+n.dist) as dist return dist,[n IN nodes(p) | n.name] as pathNodes ORDER BY dist LIMIT 5"
1) 1) "dist"
2) "pathNodes"
2) 1) 1) (integer) 12
2) "[A, D, E, G]"
2) 1) (integer) 14
2) "[A, D, C, F, G]"
3) 1) (integer) 15
2) "[A, B, E, G]"
4) 1) (integer) 16
2) "[A, D, F, G]"
5) 1) (integer) 16
2) "[A, C, F, G]"
Again, instead of traversing all possible paths, you would want to abort some traversals as soon as you are sure that they would not result in the discovery of shorter paths.
algo.SPpaths
Finding shortest paths (in kilometers) by traversing all paths and collecting the shortest ones is highly inefficient, up to the point of being impractical for large graphs, as the number of paths can sometimes grow exponentially relative to the number of relationships. Using the algo.SPpaths procedure (SP stands for single pair) you can traverse the graph, collecting only the required paths in the most efficient manner.
algo.SPpaths receives several arguments. The arguments you used in the examples above are:
-
sourceNode: the source node -
targetNode: the target node -
relTypes: list of one or more relationship types to traverse -
weightProp: the relationship’s property that represents the weight (for all specifiedrelTypes)
You are looking for minimum-weight paths. The weight of the path is the sum of the weights of all relationships composing the path. If a given relationship does not have such a property or its value is not a positive integer or float, the property defaults to 1.
The property also yields several results. The results you used in the example above are:
-
path: the path -
pathWeight: the path’s weight or sum of weightProp of all the relationships along the path
With algo.SPaths, you can solve queries like this.
Find the shortest path (in kilometers) from A to G
Set weightProp to dist:
GRAPH.QUERY g "MATCH (a:City{name:'A'}),(g:City{name:'G'}) CALL algo.SPpaths( {sourceNode: a, targetNode: g, relTypes: ['Road'], weightProp: 'dist'} ) YIELD path, pathWeight RETURN pathWeight, [n in nodes(path) | n.name] as pathNodes"
1) 1) "pathWeight"
2) "pathNodes"
2) 1) 1) "12"
2) "[A, D, E, G]"
Find the fastest path (in minutes) from A to G
Continue as before, but now set weightProp to time.
GRAPH.QUERY g "MATCH (a:City{name:'A'}),(g:City{name:'G'}) CALL algo.SPpaths( {sourceNode: a, targetNode: g, relTypes: ['Road'], weightProp: 'time'} ) YIELD path, pathWeight RETURN pathWeight, [n in nodes(path) | n.name] as pathNodes"
1) 1) "pathWeight"
2) "pathNodes"
2) 1) 1) "10"
2) "[A, D, F, G]"
Find the shortest paths (in kilometers) from A to G
GRAPH.QUERY g "MATCH (a:City{name:'A'}),(g:City{name:'G'}) CALL algo.SPpaths( {sourceNode: a, targetNode: g, relTypes: ['Road'], pathCount: 0, weightProp: 'dist'} ) YIELD path, pathWeight RETURN pathWeight, [n in nodes(path) | n.name] as pathNodes"
1) 1) "pathWeight"
2) "pathNodes"
2) 1) 1) "12"
2) "[A, D, E, G]"
In the example above, you also specified the pathCount argument, where pathCount is the number of paths to report:
-
0: retrieve all minimum-weight paths (all reported paths have the same weight) -
1: retrieve a single minimum-weight path (default) -
n>1: retrieve up to n minimum-weight paths (reported paths may have different weights)
Find 5 shortest paths (in kilometers) from A to G
GRAPH.QUERY g "MATCH (a:City{name:'A'}),(g:City{name:'G'}) CALL algo.SPpaths( {sourceNode: a, targetNode: g, relTypes: ['Road'], pathCount: 5, weightProp: 'dist'} ) YIELD path, pathWeight RETURN pathWeight, [n in nodes(path) | n.name] ORDER BY pathWeight"
1) 1) "pathWeight"
2) "[n in nodes(path) | n.name]"
2) 1) 1) "12"
2) "[A, D, E, G]"
2) 1) "14"
2) "[A, D, C, F, G]"
3) 1) "15"
2) "[A, B, E, G]"
4) 1) "16"
2) "[A, C, F, G]"
5) 1) "16"
2) "[A, D, F, G]"
Find 2 shortest paths (in kilometers) from A to G, where you can reach G in up to 12 minutes
Another interesting feature is the introduction of path constraints (‘bounded-cost’). Suppose that you want to find only paths where you can reach G in 12 minutes or less.
GRAPH.QUERY g "MATCH (a:City{name:'A'}),(g:City{name:'G'}) CALL algo.SPpaths( {sourceNode: a, targetNode: g, relTypes: ['Road'], pathCount: 2, weightProp: 'dist', costProp: 'time', maxCost: 12} ) YIELD path, pathWeight, pathCost RETURN pathWeight, pathCost, [n in nodes(path) | n.name] ORDER BY pathWeight"
1) 1) "pathWeight"
2) "pathCost"
3) "[n in nodes(path) | n.name]"
2) 1) 1) "14"
2) "12"
3) "[A, D, C, F, G]"
2) 1) "16"
2) "10"
In the example above, you added the following optional arguments:
-
costProp: the relationship’s property that represents the cost. You are looking for minimum-weight bounded-cost paths. If a given relationship does not have such property or its value is not a positive integer/float,costPropdefaults to 1. -
maxCost: the maximum cost (the bound). If not specified, there is no maximum cost constraint.
You also yielded:
pathCost: the path’s cost or the sum of costProp of all relationships along the path.
Find paths from D to G, assuming you can traverse each road in both directions
Another interesting feature is the ability to revert or ignore the relationship direction.
GRAPH.QUERY g "MATCH (a:City{name:'D'}),(g:City{name:'G'}) CALL algo.SPpaths( {sourceNode: a, targetNode: g, relTypes: ['Road'], relDirection: 'both', pathCount: 1000, weightProp: 'dist'} ) YIELD path, pathWeight RETURN pathWeight, [n in nodes(path) | n.name] as pathNodes ORDER BY pathWeight"
1) 1) "pathWeight"
2) "pathNodes"
2) 1) 1) "10"
2) "[D, E, G]"
2) 1) "12"
2) "[D, C, F, G]"
3) 1) "14"
2) "[D, F, G]"
4) 1) "17"
2) "[D, A, B, E, G]"
5) 1) "17"
2) "[D, B, E, G]"
6) 1) "18"
2) "[D, A, C, F, G]"
7) 1) "24"
2) "[D, B, A, C, F, G]"
8) 1) "27"
2) "[D, C, A, B, E, G]"
9) 1) "31"
2) "[D, E, B, A, C, F, G]"
10) 1) "41"
2) "[D, F, C, A, B, E, G]"
In the example above, you added the following optional argument:
relDirection: one ofincoming,outgoing, orboth. If not specified,relDirectiondefaults tooutgoing.
Find paths with length up to 4 from D to G, assuming you can traverse each road in both directions
Suppose you want to repeat the query above but also limit the path-length (number of relationships along to path) to 4:
GRAPH.QUERY g "MATCH (a:City{name:'D'}),(g:City{name:'G'}) CALL algo.SPpaths( {sourceNode: a, targetNode: g, relTypes: ['Road'], relDirection: 'both', pathCount: 1000, weightProp: 'dist', maxLen: 4} ) YIELD path, pathWeight RETURN pathWeight, [n in nodes(path) | n.name] as pathNodes ORDER BY pathWeight"
1) 1) "pathWeight"
2) "pathNodes"
2) 1) 1) "10"
2) "[D, E, G]"
2) 1) "12"
2) "[D, C, F, G]"
3) 1) "14"
2) "[D, F, G]"
4) 1) "17"
2) "[D, A, B, E, G]"
5) 1) "17"
2) "[D, B, E, G]"
6) 1) "18"
2) "[D, A, C, F, G]"
In the example above, you specified the following optional constraint:
maxLen: maximum path length (number of roads along the path)
algo.SSpaths
Some problems involve just one node, the source node, where you ask questions about possible paths or reachable destinations, given some constraints.
That’s what the algo.SSpaths procedure (SS stands for single source) is all about.
algo.SSpaths accepts the same arguments as algo.SPpaths, except targetNode. It also yields the same results (path, pathCost, and pathWeight).
Find all paths from A if the trip is limited to 10 kilometers
GRAPH.QUERY g "MATCH (a:City{name:'A'}) CALL algo.SSpaths( {sourceNode: a, relTypes: ['Road'], pathCount: 1000, costProp: 'dist', maxCost: 10} ) YIELD path, pathCost RETURN pathCost, [n in nodes(path) | n.name] as pathNodes ORDER BY pathCost"
1) 1) "pathCost"
2) "pathNodes"
2) 1) 1) "2"
2) "[A, D]"
2) 1) "3"
2) "[A, B]"
3) 1) "6"
2) "[A, D, C]"
4) 1) "7"
2) "[A, D, E]"
5) 1) "8"
2) "[A, B, D]"
6) 1) "8"
2) "[A, C]"
7) 1) "10"
2) "[A, B, E]"
Find all paths from A if the trip is limited to 8 minutes
GRAPH.QUERY g "MATCH (a:City{name:'A'}) CALL algo.SSpaths( {sourceNode: a, relTypes: ['Road'], pathCount: 1000, costProp: 'time', maxCost: 8} ) YIELD path, pathCost RETURN pathCost, [n in nodes(path) | n.name] as pathNodes ORDER BY pathCost"
1) 1) "pathCost"
2) "pathNodes"
2) 1) 1) "3"
2) "[A, C]"
2) 1) "4"
2) "[A, B]"
3) 1) "4"
2) "[A, D]"
4) 1) "5"
2) "[A, D, C]"
5) 1) "6"
2) "[A, D, F]"
6) 1) "6"
2) "[A, C, F]"
7) 1) "8"
2) "[A, D, C, F]"
8) 1) "8"
2) "[A, D, E]"
Find 5 shortest paths (in kilometers) from A
GRAPH.QUERY g "MATCH (a:City{name:'A'}) CALL algo.SSpaths( {sourceNode: a, relTypes: ['Road'], pathCount: 5, weightProp: 'dist', costProp: 'cost'} ) YIELD path, pathWeight, pathCost RETURN pathWeight, pathCost, [n in nodes(path) | n.name] as pathNodes ORDER BY pathWeight"
1) 1) "pathWeight"
2) "pathCost"
3) "pathNodes"
2) 1) 1) "2"
2) "1"
3) "[A, D]"
2) 1) "3"
2) "1"
3) "[A, B]"
3) 1) "6"
2) "2"
3) "[A, D, C]"
4) 1) "7"
2) "2"
3) "[A, D, E]"
5) 1) "8"
2) "1"
3) "[A, C]"
Find 5 shortest paths (in kilometers) from A if the trip is limited to 6 minutes
GRAPH.QUERY g "MATCH (a:City{name:'A'}) CALL algo.SSpaths( {sourceNode: a, relTypes: ['Road'], pathCount: 5, weightProp: 'dist', costProp: 'time', maxCost: 6} ) YIELD path, pathWeight, pathCost RETURN pathWeight, pathCost, [n in nodes(path) | n.name] as pathNodes ORDER BY pathWeight"
1) 1) "pathWeight"
2) "pathCost"
3) "pathNodes"
2) 1) 1) "2"
2) "4"
3) "[A, D]"
2) 1) "3"
2) "4"
3) "[A, B]"
3) 1) "6"
2) "5"
3) "[A, D, C]"
4) 1) "8"
2) "3"
3) "[A, C]"
5) 1) "14"
2) "6"
3) "[A, D, F]"